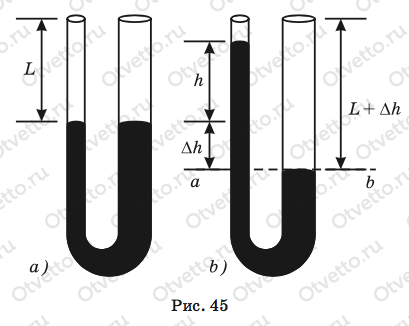
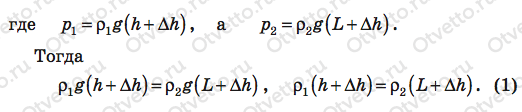Задача: В сообщающиеся сосуды разного сечения налита ртуть так, что ее уровень располагается на расстоянии L от края сосуда (рис. 45, а). Затем в широкий сосуд налили до края воду. На какую высоту h поднялся при этом уровень ртути в узком сосуде? Сечение широкого сосуда в N раз больше, чем узкого, плотности ртути ρ1 и воды ρ2 известны.
Пояснение: Обозначим р1 давление столбика ртути над уровнем ab, р2 — давление столбика воды над этим уровнем, ∆h — разность уровней ртути в широком сосуде до и после того, как туда налили воду, ∆V — объем ртути, выдавленный водой из широкого сосуда, S — площадь сечения узкого сосуда, h — высоту, на которую поднялся уровень ртути в узком сосуде, g — ускорение свободного падения.
Теперь учтем, что объем ртути ∆V, выдавленный водой из широкого сосуда, равен объему ртути, прибывшей из−за этого в узкий сосуд. Поскольку объем ∆V можно представить как произведение высоты столбика ртути на площадь поперечного сечения сосуда, то применительно к узкому сосуду, площадь сечения которого обозначим S, запишем: ∆V = hS, а применительно к широкому, площадь которого в N раз больше: ∆V = ∆hNS. Тогда hS = ∆hNS, откуда