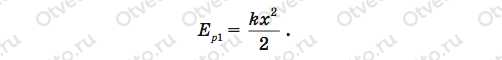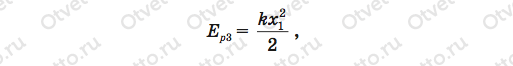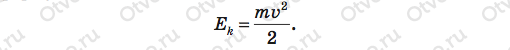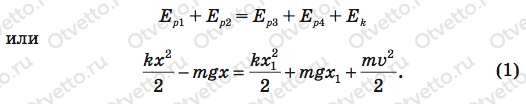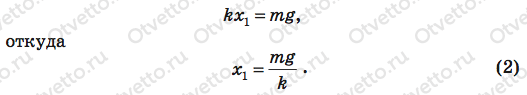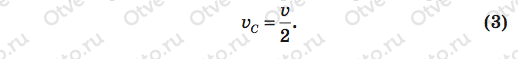Задача: Два одинаковых бруска массами по 200 г каждый соединены упругой вертикальной пружиной с жесткостью 300 Н/м (рис. 38). Нажатием на верхний брусок пружину сжали так, что ее деформация стала 5 см. Какова будет скорость центра масс этой системы тел в момент отрыва нижнего бруска от стола? Сопротивление не учитывать.
Пояснение: Обозначим m массу каждого бруска, х — деформацию пружины при сжатии, g — ускорение свободного падения, k — жесткость пружины, vc — скорость центра масс системы тел, Ер1 — потенциальную энергию сжатой пружины, Ер2 — потенциальную энергию центра масс относительно первоначального уровня, х1 — деформацию растянутой пружины, Ер3 — потенциальную энергию растянутой пружины, Ер4 — потенциальную энергию центра масс относительно первоначального положения при растянутой пружине, Еk — кинетическую энергию верхнего бруска, v — его скорость.
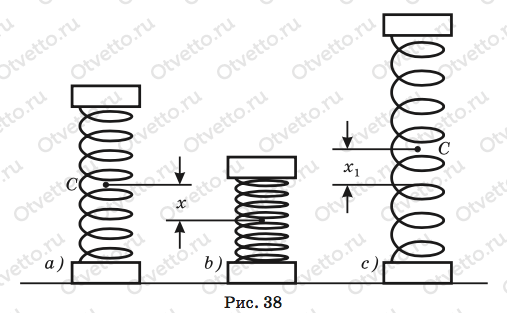
В нашем случае, поскольку система бруски — пружина симметрична, ее центр масс С располагается в геометрическом центре системы, т. е. посередине пружины.
Теперь давайте выполним рисунок. Сначала изобразим пружину недеформированной (рис. 38, а). Когда ее сжали, центр масс опустился на расстояние х относительно первоначального положения (рис. 38, b). Значит, пружина приобрела потенциальную энергию Ер1, которую можно определить по формуле
Кроме того, поскольку центр тяжести опустился на расстояние х, то относительно прежнего уровня центр масс приобрел отрицательную потенциальную энергию. Напомним, что потенциальная энергия может быть и положительной, и отрицательной, поскольку она относительна. Относительно стола потенциальная энергия центра масс положительна, поскольку он выше стола, а относительно прежнего положения — отрицательна, поскольку теперь центр масс ниже прежнего уровня. Эту потенциальную энергию Ер2 можно определить по формуле
Попробуем решить эту задачу, применив закон сохранения механической энергии. Этот замечательный закон выручит вас при решении почти любых задач динамики — особенно когда не требуется учитывать все силы, действующие в системе. Согласно этому закону суммарная механическая энергия брусков со сжатой пружиной равна их суммарной механической энергии в момент, когда нижний брусок еще лежит на столе, но пружина уже растянулась, ее деформация стала х1, центр тяжести поднялся на высоту х1 над первона- чальным положением и верхний брусок приобрел скорость vс (рис. 37, b). При этом потенциальная энергия пружины
а потенциальная энергия центра масс Ер4 относительно первоначального положения стала положительной и равной:
Кроме того, верхний брусок приобрел скорость v и, значит, кинетическую энергию Еk, которая определяется по формуле
Теперь давайте запишем закон сохранения механической энергии, а затем подумаем, какие величины нам еще надо определить, чтобы найти искомую жесткость:
Здесь нам не известны деформация х1 и скорость верхнего бруска. По закону Гука произведение жесткости пружины на ее деформацию равно деформирующей ее силе, которая в момент отрыва нижнего бруска от стола равна весу этого бруска Р = mg, поэтому мы можем записать:
Здесь уже все величины в правой части нам даны. Теперь подумаем, как выразить неизвестную скорость верхнего бруска через высоту поднятия центра тяжести, которая нам известна. Попробуем связать эту скорость со скоростью центра масс vс в этот момент. Будем рассуждать так. Нижний брусок еще покоится, его скорость равна нулю, а верхний уже получил скорость v. Значит, по мере подъема от витка к витку их скорость линейно нарастает, поэтому скорость центра масс, лежащего посередине пружины, будет равна половине скорости верхнего бруска:
Теперь давайте подставим правую часть равенства (2) в формулу (1) и из полученного выражения найдем скорость верхнего бруска v, а затем — и скорость центра масс vс :
Ответ: vс = 2,55 м/с.