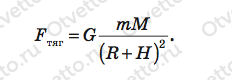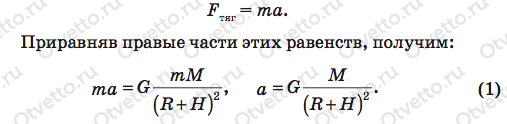Задача: Геостационарный спутник находится на высоте Н над одной и той же точкой планеты массой М, вращающейся вокруг своей оси с угловой скоростью ω. Найти среднюю плотность вещества планеты ρ.
Пояснение: Обозначим Fтяг силу тяготения спутника к планете, G — гравитационную постоянную, m — массу спутника, R — радиус планеты, а — центростремительное ускорение спутника, V — объем планеты.
На спутник массой m со стороны планеты действует сила тяготения, равная по закону всемирного тяготения:
Эта сила, согласно второму закону Ньютона, равна произведению массы спутника и его центростремительного ускорения:
Теперь свяжем центростремительное ускорение спутника с известной нам из условия задачи угловой скоростью планеты, не забывая при этом, что здесь радиусом орбиты спутника является сумма радиуса планеты и его высоты над ней:
Пока что мы еще не ввели нужную нам плотность в наши формулы. Но смотрите: из последнего выражения нетрудно найти радиус планеты R, а через него выразить ее объем. Зная же объем планеты и ее массу, уже легко найти плотность планеты по формуле
Нам осталось из равенства (3) выразить радиус планеты и подставить его в правую часть выражения (4). Проделаем эти действия: