В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h (рис.). Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.
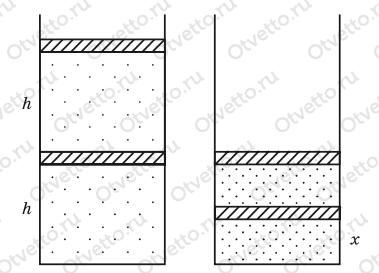
Обозначим h расстояние от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего, х — расстояние х от нижнего поршня до дна сосуда после сжатия, ратм — атмосферное давление, р1 — давление газа под верхним поршнем, рп — давление поршня, V1 — объем воздуха под верхним поршнем вначале, S — площадь основания поршней и дна цилиндра, р2 — давление под верхним поршнем после опускания верхнего поршня на место нижнего, рс — давление силы, придавившей поршень, V2 — новый объем воздуха под верхним поршнем, р3 — давление газа под нижним поршнем до опускания верхнего, р4 — давление газа под нижним поршнем после его сжатия, Т3 — объем воздуха под нижнем поршнем после сжатия.

Закон Бойля — Мариотта применительно к газу подверхним поршнем будет выглядеть так:
p1V1=p2V2. (1)
Давление газа под верхним поршнем р1 при равновесии равно сумме атмосферного давления ратм и давления поршня рп:
р1 = ратм + рп
Но по условию задачи р1 = 2ратм, поэтому 2ратм = ратм + рп, откуда
рп = ратм. (2)
Объем воздуха под верхним поршнем вначале был равен:
V1 = hS. (3)
После опускания верхнего поршня на место нижнего газ под ними сжался и давление под верхним поршнем стало р2. Теперь оно равно сумме давлений атмосферы ратм, поршня рп и некоторой силы, придавившей поршень, рс:
р2 =ратм +рп +рс
или с учетом (2)
р2 = 2ратм + рс. (4)

Теперь нам предстоит решить систему уравнений (6) и (11) относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов — может, мы их при этом немного упростим. Начнем с уравнения (6)

Ответ: х = 0,55h.
