Задача: Горизонтальная платформа равномерно вращается вокруг вертикальной оси, проходящей через ее центр. На расстоянии, равном трети радиуса платформы, отрывается от ее поверхности небольшое тело и скользит по ней без трения. Через сколько времени тело слетит с платформы, если до отрыва оно двигалось с ускорением 0,1 м/с^2? Радиус платформы 60 см.
Решение:
Обозначим а — ускорение тела, R — радиус платформы, t — время, через которое тело слетит с платформы, v — линейную скорость тела на платформе, S — путь, который пройдет тело.
Чтобы легче представить движение тела по платформе, выполним чертеж (рис. 15). Посмотрим на платформу сверху и нарисуем круг, покажем его центр О и проведем горизонтальный радиус R. Затем на расстоянии, равном трети радиуса от края платформы, изобразим тело в точке М в момент отрыва. Значит, в этот момент от тела до центра платформы расстояние составило две трети радиуса.
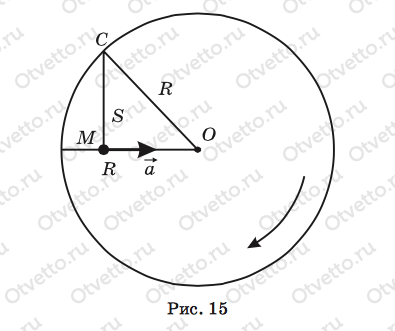
Теперь давайте думать. Нам известно ускорение тела а перед отрывом от поверхности платформы. Но платформа вращается равномерно, значит, это его центростремительное ускорение. В момент отрыва линейная скорость тела v направлена по касательной к окружности, по которой оно двигалось до отрыва. Радиус этой окружности составлял
(2/3)R . А мы знаем формулу, связывающую линейную скорость с центростремительным ускорением. Применительно
к нашей задаче она будет выглядеть так:
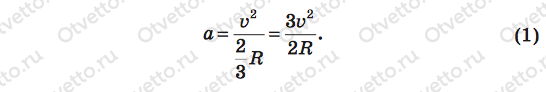
После отрыва тело станет двигаться к краю платформы без трения. Значит, это движение будет равномерным и прямолинейным со скоростью v. Тогда тело слетит с платформы в точке С, проделав путь S. Если этот путь разделить на линейную скорость тела, мы найдем искомое время t, через которое тело слетит с платформы:
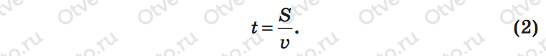
Дальнейший ход решения ясен. Путь S находим из прямоугольного треугольника МСО по теореме Пифагора, а линейную скорость v — из выражения (1), и все это подставляем в равенство (2). Приступим. По теореме Пифагора
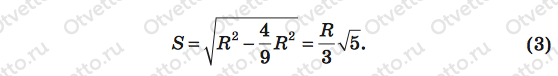
Теперь из (1) находим линейную скорость v:
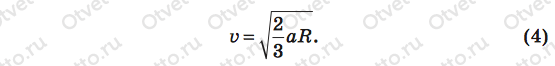
Нам осталось подставить правые части равенств (3) и (4) в формулу (2), и задача в общем виде будет решена. Подставляем:
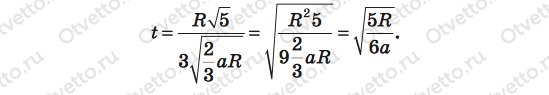
Задача в общем виде решена. Подставим числа и вычислим. 60 см = 0,6 м.
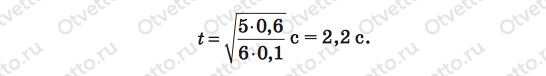
Ответ: 2,2 c.
